八种排序算法

数据结构与算法

排序Sort

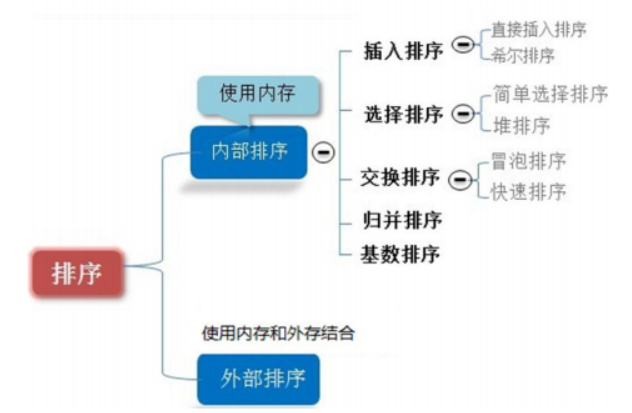
其中：

一轮结束后能够确定一个元素的最终位置的排序方法有是 简单选择排序、快速排序、冒泡排序、堆排序。

1. 冒泡排序BubbleSort

冒泡排序思路：

• 每次遍历数组，都会比较相邻元素的大小，如果满足条件，就把两个元素交换位置。

• 这样，每遍历一遍数组，都会把最大或最小的元素放在数组尾部，就像气泡上浮一样。

• 显然，如果有m个数，则最多要遍历m-1次。

优化：

• 在一轮遍历中，我们无需再比较最后一个数，所以每轮遍历要比较m-1次

• 而在一轮遍历中，我们还无需再比较前几轮遍历产生的“尾泡”

  • 如果遍历n轮，就会产生n个“尾泡”，所以，在此轮遍历中只需要比较m-1-n次

• 如果在某轮遍历中，发现遍历的数组依然有序，这时可以不再进行下轮遍历

  • 我们只需要加一个，标志数组是否发生过交换的变量，根据变量判断数组是否已经有序

实现很简单，如：

package Sort;
import java.util.Arrays;

public class BubbleSorting {
    //冒泡排序方法
    public int[] bubbleSort(int[] array) {
        int temp;
        //标识此次排序是否发生改变
        boolean isChanged = false;
        //开始排序
        for (int n = 0; n < array.length - 1; n++) {
                //把最大的数浮动到末尾，i循环到array.length-1即可，因为i为倒数第二时，会比较array[i]和array[i+1]，
                //此时倒数第一的数已经比较过了，也防止数组越界
                for (int i = 0; i < array.length - 1 - n; i++) {
                    //开始本次冒泡前，把isChanged置为false
                    //如果前面的数比后面的数大，交换位置
                    if (array[i] > array[i + 1]) {
                        temp = array[i];
                        array[i] = array[i + 1];
                        array[i + 1] = temp;
                        //位置发生变化，把isChanged置为true
                        isChanged = true;
                    }
                }
                //for检查一遍数组后，发现isChanged的值未变化
                if (!isChanged){
                    //退出循环
                    break;
                }else {
                    //把isChanged改回来
                    isChanged=false;
                }
                System.out.println(Arrays.toString(array));
        }
        return array;
    }
}

class BubbleSortingTest {
    public static void main(String[] args) {
        int[] arr = {5, 7, 4, 6, 3, 1, 2, 9, 8};
        BubbleSorting bubbleSorting = new BubbleSorting();
        int[] sorted = bubbleSorting.bubbleSort(arr);
    }
}

2. 快速排序QuickSort

快速排序采用了分而治之的思想：

• 通过一个基准数pivot来把整个数组分成两部分，一部分全大于pivot，一部分全小于pivot，然后把pivot放在这两部分中间，这样就找到了pivot的正确位置。
• 然后再对每个部分再次进行同样的分割，通常使用递归来实现，一直到不能再分割为止。
• 这样分割完成后，就得到一个有序的数列。

这里，我们通过两个指针来对数组array进行分割：

• 取数组最后一个数为基准数pivot，其下标为pivotIndex
• 设一个快指针quickP，它会遍历数组从左端到pivot之前的所有数，不包括pivot
• 设一个慢指针slowP，它只在快指针发现当前数小于基准数时移动1次，慢指针从数组左端-1开始。
• 慢指针slowP移动后，会把array[slowP]与array[quickP]交换
• 当快指针quickP遍历完成后，交换array[slowP+1]与array[pivotIndex]，这样就把pivot放在了正确的位置。
• 可以看这个视频，能够方便理解：图解快速排序，也可以直接看代码，我注释很多

java实现

package Sort;

import java.util.Arrays;

public class QuickSorting {

    //快指针，始终移动
    int quickP = 0;
    //慢指针，当快指针满足条件时移动
    int slowP;
    //基准数、中间点
    int pivot;
    //基准数所在位置
    int pivotIndex;
    //temp交换的中间变量
    int temp;


    /**
     * 用于分割数组
     *
     * @param array 待分割数组
     * @param left  数组左端点
     * @param right 数组右端点
     */
    public int partition(int[] array, int left, int right) {
        //慢指针初始位置是左端点的前一个点
        slowP = left - 1;
        //设数组最后一个数为基准数
        pivot = array[right];
        pivotIndex = right;
        //在数组头到基准数之间遍历
        for (quickP = left; quickP < pivotIndex; quickP++) {
            //若发现当前数比基准数小
            if (array[quickP] < pivot) {
                //慢指针后移
                slowP += 1;
                //把快指针的数与慢指针的数交换位置
                temp = array[quickP];
                array[quickP] = array[slowP];
                array[slowP] = temp;
            }
        }
        //退出循环后，交换slowP+1和基准数，这样通过slowP+1把数组分为了两部分
        temp = array[slowP + 1];
        array[slowP + 1] = array[pivotIndex];
        array[pivotIndex] = temp;
        return slowP + 1;
        //于是数组分成的两部分为：[left,slowP+1-1]、[slowP+1+1,right]
    }

    /**
     *递归分割来完成排序
     * @param array 待分割数组
     * @param left  数组左端点
     * @param right 数组右端点
     */
    public void quickSort(int[] array, int left, int right) {
        //不停分割数组，直到最后分成的数组左端点=右端点
        if (left >= right) {
            return;
        }
        //接收分割完成后的中点下标，中点不再参与分割和排序
        pivotIndex = partition(array, left, right);
        //左边的数组：[left,pivotIndex-1]
        quickSort(array, left, pivotIndex - 1);
        //右边的数组：[pivotIndex+1,right]
        quickSort(array, pivotIndex + 1, right);
    }

}

//测试
class QuickSortingTest {
    public static void main(String[] args) {
        int[] array = {0, 7, 4, 6, 3, 1, 2, 9, 8, 5};
        QuickSorting quickSorting = new QuickSorting();
        quickSorting.quickSort(array, 0, array.length - 1);
        System.out.println(Arrays.toString(array));
    }
}

3. 选择排序SelectionSort

选择排序每轮遍历数组，会把数组中的最值放在数组头部或尾部，即每轮都会找到一个最小的数或最大的数。

显然，选择排序与冒泡排序思路类似，都是每轮遍历找到一个最值，只是交换的方式有区别。

我们只需关注这一点即可：

• 冒泡排序是依次比较，把符合条件的两个相邻元素交换位置，这样把最值交换到末尾
• 选择排序，是假定一个数是最值，然后依次与数组中的数据比较，让满足条件的数替换这个假定的数，一轮遍历完成后，再让它与当前数组尾或头部的数交换

很简单，不需要细说。

java实现

如：

package Sort;

import java.util.Arrays;

public class SelectSorting {

    //一轮遍历中的最小值
    private int minValue;
    //最小值的下标
    private int minIndex;
    //交换位置时，需要的中间量
    private int temp;
    //标识最小数是否发生改变、
    private boolean minIsChanged=false;

    public int[] SelectSort(int[] array) {

        //遍历n轮
        for (int n = 0; n < array.length; n++) {
            //取当前轮次的数组第一个数为最小数，并记录其下标
            minIndex = n;
            minValue = array[minIndex];
            //一轮中的遍历，i从当前轮次数组的第二个数开始
            for (int i = n + 1; i < array.length ; i++) {
                //若数组中有比minValue还小的数，把它赋给minValue，并记录下标，然后标识出最小值已经改变
                if (array[i] < minValue) {
                    minIndex = i;
                    minValue = array[minIndex];
                    minIsChanged=true;
                }
            }
            //一轮遍历完毕，将得到的最小数与当前轮数组的第一个数交换位置
            //若最小值没有变化，即minIsChanged为false时，不需要交换
            if (minIsChanged){
                temp = array[minIndex];
                array[minIndex] = array[n];
                array[n] = temp;
            }
        }
        //排序完成后打印数组
        System.out.println(Arrays.toString(array));
        return array;
    }
}
class SelectSortingTest{
    public static void main(String[] args) {
        int[] array={5, 7, 4, 6, 3, 1, 2, 9, 8};
        SelectSorting selectSorting=new SelectSorting();
        selectSorting.SelectSort(array);
    }
}

4. 插入排序InsertionSort

插入排序把数组分为两个部分，一部分视为有序，初始只有一个元素；另一部分是无序，包含其他的数组元素

• 在每轮遍历时，取出无序部分的数，经过比较后插入到有序部分中，使有序部分仍然有序。

• 随着每轮的遍历，无序部分的数被插入到有序部分中，最终，只剩下一个有序的数组。

主要的难点在于如何找到有序部分的插入位置，并将有序的一部分数后移，先看第一种实现：

java实现①

public int[] insertSort(int[] array) {
       //从array[0]到array[n]是有序部分
       //从array[n+1]到末尾，是无序部分
       for (int n = 0; n < array.length-1; n++) {
           //取出一个无序部分头部的数，注意，此时该位置的数据可以视为“空”
           disOrderNum = array[n + 1];
           //遍历有序部分进行比较和执行插入
           for (int i = 0; i < n + 1; i++) {
               //若取出的无序数比某个有序数小，把它放在这个有序数的前面
               if (disOrderNum < array[i]) {
                   //把有序部分最末尾的数后移1位 （相当与，此时把有序的末尾，放在无序的头部）
                   array[n + 1] = array[n];
                   //把i以后的有序数后移1位
                   for (int j = n; j > i; j--) {
                       array[j] = array[j - 1];
                   }
                   //插入无序数
                   array[i] = disOrderNum;
                   //进入下一轮循环
                   break;
               }
           }
       }
       System.out.println(Arrays.toString(array));
       return array;
   }

这里使用3个for循环嵌套，显然，是非常耗费性能的。我们对有序数后移这部分，进行优化：

• 我们可以在比较大小时，就把有序数后移

java实现②

//优化
    public int[] insertSort2(int[] array) {
        //从array[0]到array[n]是有序部分
        //从array[n+1]到末尾，是无序部分
        for (int n = 0; n < array.length - 1; n++) {
            //取出一个无序部分头部的数，注意，此时该位置的数据可以视为“空”
            disOrderNum = array[n + 1];
            //遍历有序部分进行比较和执行插入
            int index;
            //指针，从有序部分尾部开始遍历，此时n+1的位置是可以被有序部分利用的空间，可以视为有序部分末尾
            index = n + 1;
            while (true) {
                //当index到达有序部分头部，或待插入数找到合适位置时
                if (index == 0 || disOrderNum > array[index - 1]) {
                    //从后向前遍历，与下一个值比较，插入到当前位置
                    array[index] = disOrderNum;
                    break;
                }
                //把有序数的位置后移
                array[index] = array[index - 1];
                index--;
            }
        }
        System.out.println(Arrays.toString(array));
        return array;
    }

5. 希尔排序ShellSort

希尔排序是插入排序的一个更高效的改进版本，又称缩小增量排序

排序流程示意图：

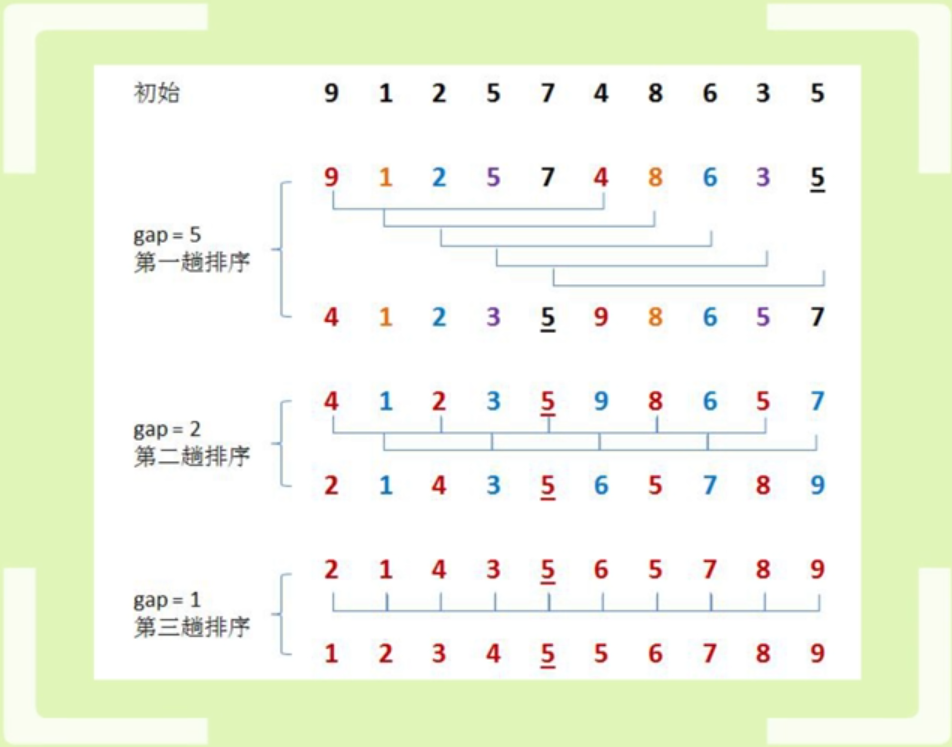
它事先以一个可变增量对数据分组，然后在对每组进行插入排序。

• 第一次分组：增量为arrary.length/2

• 第二次分组：增量为arrary.length/4

• 第n次分组：增量为arrary.length/2n

这里增量可以看作两个数下标的差值，直到增量为1时，此时只有一组数据，不再分组。

tips：

增量可以自定，只要保证增量能递减，并且最后的值是1就可以。

所以为了避免分组后的数据仍然有序的最坏情况，我们可以使用：

Hibbard增量序列：第n个增量值=2的n次方-1

或者Sedgewick增量序列，可以处理上万的数据。

这是比较简单的算法，我们只需要在分组后使用插入排序即可：

图解，对照代码来理解，ABC为3个分组：

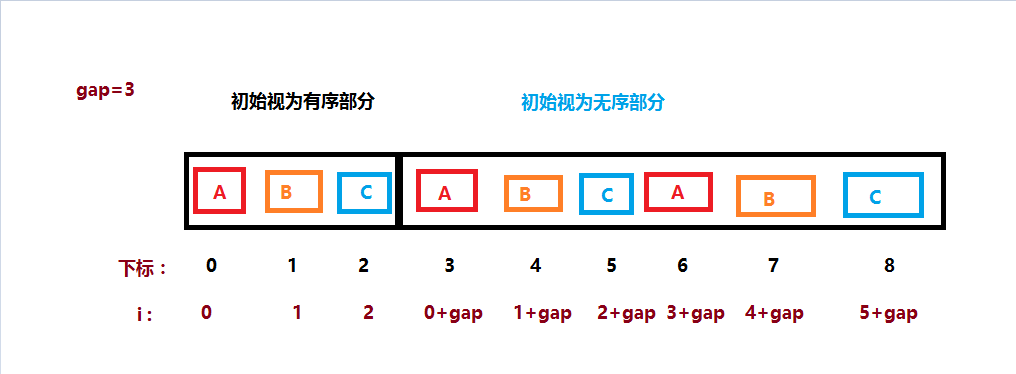
java实现

//排序1
    public void shellSort1(int[] array) {

        //用于改变增量的for循环
        for (int gap = array.length / 2; gap >= 1; gap = gap / 2) {
            //n从0开始，array[n+gap]是第n个分组的第二个元素，即第一个待插入元素，插入到array[n]那一部分中
            for (int i = gap; i < array.length; i++) {
                //所以这里i初始=0+gap意为第1个分组的第2个元素，随着i的增加，i就=1+gap、2+gap....n+gap，会遍历所有分组的第一个元素以后的所有元素。
                // 所以这个for循环是为了拿到所有待插入元素
                int j = i;
                //存储待插入元素，array[j]表示各个分组待插入到有序部分的元素
                int temp = array[j];
                //使用j来倒序遍历各个分组的有序部分
                while (true) {
                    //当待插入数大于前一个数时，找到插入的位置，插入后，退出循环
                    if (j - gap < 0 || temp > array[j - gap]) {
                        array[j] = temp;
                        break;
                    }
                    //没找到位置时，将分组中的数后移
                    array[j] = array[j - gap];
                    //j以gap为间隔，以此来遍历分组
                    j -= gap;
                }
            }
        }
//        System.out.println(Arrays.toString(array));
    }

另外一种思路：

• 这是增量gap的for循环：

for (int gap = array.length / 2; gap >= 1; gap = gap / 2) {}

• 会得到gap个分组

//比如array[1]和array[1+gap]、array[1+2*gap]是一组的
//比如array[2]和array[2+gap]、array[2+2*gap]是另外组的
for (int i = 0; i < gap; i++){}

• 遍历每个分组

for (int j = i + gap; j < array.length; j = j + gap) {}

完整代码

public void shellSort(int[] array) {

        //用于改变增量的for循环
        for (int gap = array.length / 2; gap >= 1; gap = gap / 2) {
            //使用增量对数据分组，显然有gap个需要处理的组，这是遍历出每组的for循环
            //比如array[1]和array[1+gap]、array[1+2*gap]是一组的
            //比如array[2]和array[2+gap]、array[2+2*gap]是另外组的
            for (int i = 0; i < gap; i++) {
                //对当前所在的组进行插入排序，我们这里先采用交换的方式
                //显然，如果把j每轮递增的值设为gap，那么就可以用array[j]来表示当前分组中数
                for (int j = i + gap; j < array.length; j = j + gap) {
                    //临时保存当前值
                    int temp = array[j];
                    //指针，初始值为当前数的前一个数的位置，递减
                    int preIndex = j - gap;
                    //下面的代码会把array[preIndex]和array[j]交换
                    while (true){
                        if (preIndex<0){
                            break;
                        }
                        if (array[preIndex]<temp){
                            break;
                        }
                        //把当前指向的值赋给后一位
                        array[preIndex+gap]=array[preIndex];
                        //指针前移，只会移动1次
                        preIndex=preIndex-gap;
                    }
                    //当退出循环时，preIndex会在一开始的array[preIndex]之前
                    array[preIndex+gap]=temp;

                }
            }
        }
//        System.out.println(Arrays.toString(array));
    }

6. 归并排序Mergesort

归并排序的核心思想是：

• 把两个有序数组(实际上，这两个有序数组其实是整个数组的一部分)，通过第三个temp数组，合并为新的有序数组。

而如何获得这两个有序数组呢？

• 将待排的无序数组不停拆分，直到不可再拆，这样就得到一个个只包含1个元素的数组，我们可以把它视为有序数组。

显然，归并排序也使用了分而治之的思想。

归并的图解：

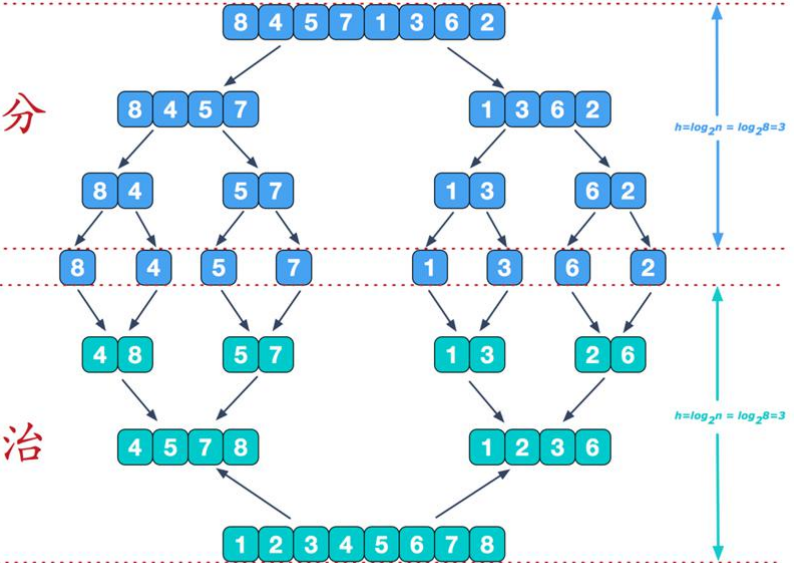
具体实现：

• 先看两个有序数组的合并

①设两个指针i与j来遍历各自的数组部分，下图用绿色和红色来表示两个部分，它们的初始位置都在各自部分的头部。依次比较i与j对应的值，把较小的一方放入一个temp临时数组，当指针指向的值已经被放入temp后，对应指针后移，temp的指针也后移，以此类推：

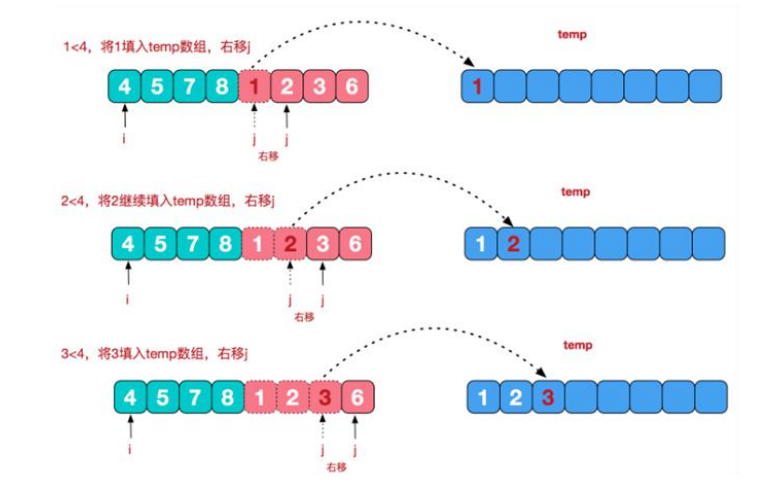
②当绿色或者红色部分有一方的数已经全放入了temp，那么把另一部分的数一次性全放入temp中，如此，这两部分的数就已经全放入到temp中了，最后，把temp中的数再复制回去，覆盖掉，这样就结束了本次合并，得到了一个有序数组。

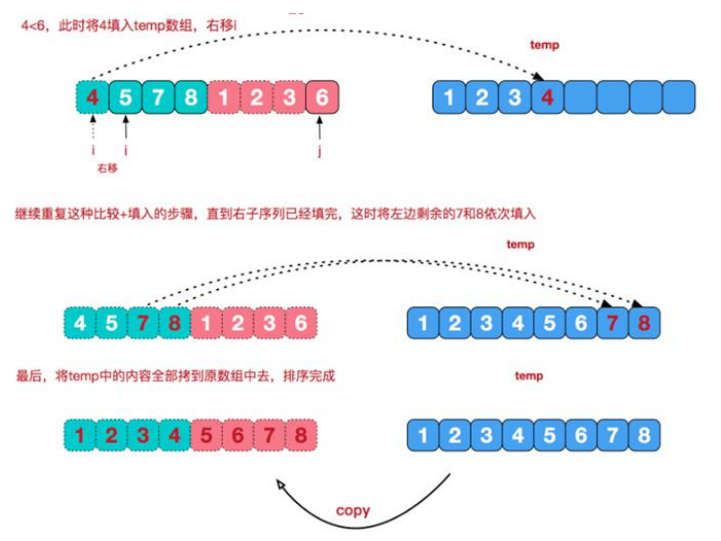
• 拆分阶段较为简单，只需要直到每次要拆分的数组的左端点left和右端点right，就可以得到中间点pivot，这样会得到[left,pivot]和[pivot+1,right]这两部分数组，然后把对应数组再次拆分即可

代码实现1

package Sort;

import java.util.Arrays;

public class MergeSorting {
    
    public void merge1(int[] array, int[] temp, int left, int pivot, int right) {
        //temp的指针
        int t=0;
        //这样原数组就分为两个有序部分，[left,pivot],[pivot+1,right]
        //指向前部分的头部
        int leftP1 = left;
        //指向后部分的头部
        int leftP2 = pivot + 1;
        //直到有一部分的指针已经走到尾部
        while (leftP1 <= pivot && leftP2 <= right) {
            //若前部分的指针，所在位置的值比另外一个指针的小，把对应值存到temp数组中，
            // 然后前部分的指针和temp的指针后移
            if (array[leftP1] <= array[leftP2]) {
                temp[t] = array[leftP1];
                leftP1++;
                t++;
                //否则就是后部分的指针的值小
            } else {
                temp[t] = array[leftP2];
                leftP2++;
                t++;
            }
        }
        //把后部分指针的剩余数，全放入temp
        while (leftP1 <= pivot) {
            temp[t] = array[leftP1];
            t++;
            leftP1++;
        }
        //把前部分指针的剩余数，全放入temp
        while (leftP2 <= right) {
            temp[t] = array[leftP2];
            t++;
            leftP2++;
        }
        //把temp的值导入array
        t=0;
        for (int leftP=left;leftP<=right;leftP++){
            array[leftP]=temp[t];
            t++;
        }

    }

    public void mergeSort(int[] array, int[] temp, int left, int right) {
        //当left<right的时候就一直拆分
        if (left < right) {
            int pivot = (left + right) / 2;
            mergeSort(array, temp, left, pivot);
            mergeSort(array, temp, pivot+1, right);
            merge(array,temp,left,pivot,right);
        }
    }
}

class MergeSortingTest {
    public static void main(String[] args) {
        MergeSorting mergeSorting = new MergeSorting();
        int[] array = {5, 7, 4, 6, 3, 1, 2, 9, 8, 0};
        int[] temp = new int[array.length];
        mergeSorting.mergeSort(array, temp, 0, array.length-1);
        System.out.println(Arrays.toString(array));
    }
}

上个代码中，使用了temp作为临时数组，最后每次归并又把temp写回了array，我们可以调整一下思路，能不能把要合并的两部分作为新数组，然后直接与array进行交换呢？

• 这样似乎并不能优化什么，不过我觉得这样好理解一些。

代码实现2

	public void merge2(int[] array, int left, int pivot, int right) {
        //这样就得到了pivot的左右两部分
        int[] arrayLeft = Arrays.copyOfRange(array, left, pivot + 1);
        int[] arrayRight = Arrays.copyOfRange(array, pivot + 1, right + 1);
        //这两个数组的指针
        int leftP = 0;
        int rightP = 0;
        //原数组的指针arrayP
        int arrayP = left;
        //当两数组有任何一个走到头时
        while (leftP < arrayLeft.length && rightP < arrayRight.length) {
            //把两数组比较后的较小数，放入原数组，较小数的数组指针后移，原数组指针后移
            if (arrayLeft[leftP] <= arrayRight[rightP]) {
                array[arrayP] = arrayLeft[leftP];
                leftP++;
                arrayP++;
            } else {
                array[arrayP] = arrayRight[rightP];
                rightP++;
                arrayP++;
            }
        }

        //如果左部分还有数据
        while (leftP < arrayLeft.length) {
            array[arrayP] = arrayLeft[leftP];
            leftP++;
            arrayP++;
        }
        //如果右部分还有数据
        while (rightP < arrayRight.length) {
            array[arrayP] = arrayRight[rightP];
            rightP++;
            arrayP++;
        }
    }

    public void mergeSort2(int[] array,int left,int right){
        if (left<right){
            int pivot=(left+right)/2;
            mergeSort2(array,left,pivot);
            mergeSort2(array,pivot+1,right);
            merge2(array,left,pivot,right);
        }
    }

class MergeSortingTest {
    public static void main(String[] args) {
        MergeSorting mergeSorting = new MergeSorting();
        int[] array = {5, 7, 4, 6, 3, 1, 2, 9, 8};
        mergeSorting.mergeSort2(array, 0,array.length - 1);
        System.out.println(Arrays.toString(array));
    }
}

其中，合并部分还可以这样写：

public void merge2_1(int[] array, int left, int pivot, int right) {
        //这样就得到了pivot的左右两部分
        int[] arrayLeft = Arrays.copyOfRange(array, left, pivot + 1);
        int[] arrayRight = Arrays.copyOfRange(array, pivot + 1, right + 1);
        //这两个数组的指针
        int leftP = 0;
        int rightP = 0;
        //原数组的指针arrayP
        int arrayP;
        //遍历原数组的同时
        for (arrayP=left;arrayP<=right;arrayP++){
            if (rightP==arrayRight.length){
                array[arrayP] = arrayLeft[leftP];
                leftP++;
                continue;
            }
            if (leftP==arrayLeft.length){
                array[arrayP] = arrayRight[rightP];
                rightP++;
                continue;
            }
            if (arrayLeft[leftP] <= arrayRight[rightP]) {
                array[arrayP] = arrayLeft[leftP];
                leftP++;
            } else {
                array[arrayP] = arrayRight[rightP];
                rightP++;
            }
        }

    }

7. 基数排序RadixSort

基数排序是分配式的，它额外使用多个数组来存放对象，当数据量较大时，就会占用较高的内存。

核心思想：

• 借助10个数组(也可称为桶)，分别把待排数据的个位、十位、百位….排成有序，直到最高位排完，最终便得到1个有序数组

流程：

• 第一轮按照对象的个位数值，分配给对应数组，比如12分配给2号数组，200分配给0号数组，分配完毕后，将数组里的数据再依次覆盖进原数组中。
• 第二轮和上一轮类似，这次是按照十位数值
• 第三轮按照百位数值
• 直到最高位数排完为止。

我们可以使用一个二维数组表示这10个数组，不过要知道，实际上java是没有二维数组的，java的二维数组是由一维数组组成的。

• 设待排数组为array，使用int[10][array.length]表示10个数组（桶）

那么如何知道我们需要进行多少轮呢，这与原数组的最大数的位数有关

• 先对原数组进行一轮遍历，找到最大的数，假设是123，(123+"").length这样就可以巧妙的拿到一个数字的位数
• 当然，你也可以像我代码中那样，设一个布尔值的标识，使它在原数组的数据全被分入一个桶中时变化，从而停止循环。

如何拿到当前数的当前位的值

• 可以这样：int cur=(value / (n * 10)) % 10;从而拿到value个位十位…的值，n初始为1，每轮分配后变为原来的10倍。

如何表示表示这10个数组（桶）、及其指针

• 桶是按照数据的个位、十位、百位…的值(设为cur)来分配数据的，这正是设计10个桶的原因，所以cur对应为桶的下标
• 我们用一个二维数组来表示这10个桶：int[][] buckets = new int[10][];
• 使用一个一维数组表示这10个桶的指针：int[] bucketPs = {-1, -1, -1, -1, -1, -1, -1, -1, -1, -1};，下标刚好对应这10个桶，10个指针的初始值是-1，表示桶中没有数据
• 那么，bucketPs[cur]是第cur号桶的指针，buckets[cur][bucketPs[cur]]就能表示当前数据应该存入的桶及其指针位置

✭如何保证上次排序后的结果在下轮分配排序时仍然有序？

• 在把桶内数据写回原数组时，我们应该从头部开始，按照当时放入桶的顺序，对桶遍历，如果从尾部倒序遍历，就会逆序上次的排序结果。
• 可以将桶的指针的值通过temp临时保存，然后让桶指针从头开始，遍历到temp，结束一轮写回后，记得把桶指针置为初始状态。
• 也可以使用栈，利用栈把桶内数据再次逆序输出。
• 你也可以直接做个for循环，从0遍历到桶指针。

java实现

package Sort;

import java.util.Arrays;

public class RadixSorting {

    //10行数组
    int[][] buckets = new int[10][];
    //每个数组的指针，用一个一维数组来表示，10个指针初始均为-1，下标刚好对应桶的序号
    int[] bucketPs = {-1, -1, -1, -1, -1, -1, -1, -1, -1, -1};
    //原数组指针
    int arrayP;
    //变量n，用于控制位数切换，通过 (对象/n*10)%10 来拿到当前位的值，初始n为1，最大为
    int n;
    //标识是否已经排完了最高位，初始为false
    boolean flag;

    //排序方法
    public void radixSort(int[] array) {
        if (array == null) {
            System.out.println("待排数组不能为空");
            return;
        }
        //初始化这10个数组
        for (int i = 0; i < 10; i++) {
            buckets[i] = new int[array.length];
        }

        int n = 1;
        //标识是否已经排完了最高位，初始为false
        boolean flag = false;
        while (true) {
            //n递增
            n=n*10;
            //遍历原数组
            for (int value : array) {
                //得到当前数，当前位的值，index在我的文档里是cur
                int index = (value / (n * 10)) % 10;
                //放到值对应的数组里,第index号桶，第index号桶的指针自增
                buckets[index][++bucketPs[index]] = value;
                //当发现把待排数全部都放入了一个桶中，也就是这个桶的指针为待排数组的长度-1时，这表示最高位的数已经被排完或者不用再排了
                if (bucketPs[index]==array.length-1) flag=true;
            }
            //如果发现已经排完，则退出循环
            if (flag) break;
            //分配完成后，把桶里的数覆盖回原数组，注意要让桶指针从头部到尾的顺序输出，否则会使上一次的排序逆序
            //重置原数组的指针
            arrayP = 0;
            int tempP;
            //从0号桶开始，一个个遍历这10个桶,buckets.length直接写成10也没问题
            for (int i = 0; i < buckets.length; i++) {
                //记录当前桶指针的位置
                tempP = bucketPs[i];
                //把桶指针置为头部
                bucketPs[i] = 0;
                //开始循环
                while (arrayP < array.length) {
                    //当当前桶的指针小于0时，或者大于循环前的位置时，退出当前桶的循环，换到下一个桶
                    if (bucketPs[i] < 0 || bucketPs[i] > tempP) {
                        //此时当前桶的指针为-1，刚好为初始状态
//                   bucketPs[i] = -1;
                        break;
                    }
                    //把当前桶的数一一拿出，赋给原数组
                    array[arrayP] = buckets[i][bucketPs[i]];
                    //把已经被取出的数据置为0方便debug
                    buckets[i][bucketPs[i]] = 0;
                    //桶指针后移
                    bucketPs[i]++;
                    //原数组指针后移
                    arrayP++;
                }

            }
            //一轮分配完成，重置桶的指针
            bucketPs = new int[]{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1};
            System.out.println();

        }
    }

}
//测试
class RarixSortingTest {
    public static void main(String[] args) {
        int[] array = {1, 131, 2342, 312, 4987, 525, 6453, 732, 89};
        RadixSorting radixSorting = new RadixSorting();
        radixSorting.radixSort(array);
        System.out.println(Arrays.toString(array));
    }
}

输出结果

[1, 89, 131, 312, 525, 732, 2342, 4987, 6453]

Process finished with exit code 0

8.堆排序Heapsort

堆排序需要堆这种数据结构，

堆的概念

由于我之前的文章并没有讲到树和堆的数据结构，所以在这里说一下主要的概念：

二叉树大家应该都知道，而堆和树关系密切，堆需要满足以下两个条件：

1. 满足完全二叉树
2. 每个父结点都大于或都小于子结点

什么是完全二叉树

看下几个图就明白了：

这个是完全二叉树：

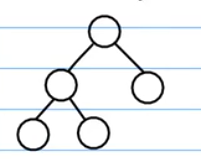
这个也是完全二叉树：

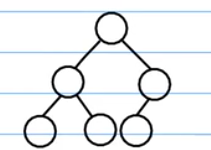
这个不是完全二叉树：

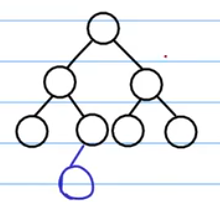
堆的两种分类

注意父结点与子结点值之间的关系：

大顶堆（大根堆）

小顶堆（小根堆）

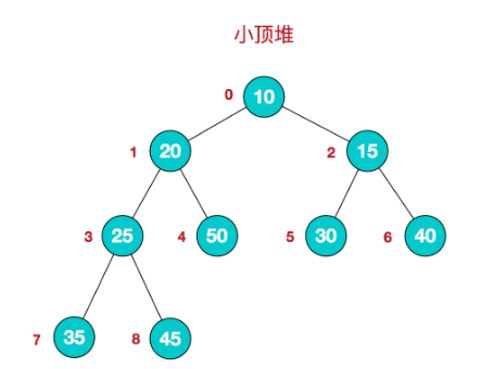
构建堆

在这之前，要说明一下堆的数组存储

堆的数组存储

堆的数组存储就是树的数组存储，从父结点的位置0开始，依次为结点编号，从左到右，从上到下，然后将树用数组的形式表示即可，每个数组元素对应该位置编号的节点，如上图所示，array[8]==45，array[0]==10。

设index为从0开始的位置编号，对应数组下标，则一个index为i的节点，它与父结点、子结点的关系，将满足以下条件：

• 父结点：parentNode=(i-1)/2
• 左子结点：childNodeLeft=2i+1
• 右子结点：childNodeRight=2i+2

堆化逻辑

将一个无序二叉树，转为大顶堆或小顶堆的过程叫做堆化(heapify)

依次将两个子结点和父结点进行比较，每次比较，都选出一个较大的结点，与父结点交换位置，便可以找出最大的结点作为新的父结点。对每个子树都做这种处理后，就可以形成一个大顶堆；反之选较小的节点，便会形成小顶堆

对一个节点所在的子树做heapify的时候，必须保证此节点的所有子树都已经是堆，一般从二叉树的倒数第二层开始做heapify，从最后一个非叶子节点开始，具体为：

//数组形式存储的树
int[] treeArray={4,10,3,5,1,2...};
//拿到最后一个节点的下标
int lastNodeIndex = treeArray.length-1;
//找到最后一个节点的父结点 从此节点开始向上堆化即可
int lastParentIndex=(lastNodeIndex-1)/2;

堆化的代码实现

仔细看注释

java

package Sort;

import java.util.Arrays;

public class HeapSorting {


    /**
     * 交换两个结点的位置
     *
     * @param treeArray 一个数组
     * @param index     数组位置1
     * @param maxIndex  数组位置2
     */
    public void swap(int[] treeArray, int index, int maxIndex) {
        //临时变量
        int temp = treeArray[index];
        treeArray[index] = treeArray[maxIndex];
        treeArray[maxIndex] = temp;
    }


    /**
     * 堆化核心方法 堆化子树 大顶堆 对一个节点做heapify的时候，必须保证它的所有子树都已经是堆。
     * @param treeArray 数组形式的树
     * @param index     从index号位开始堆化
     */
    public void heapify(int[] treeArray, int index) {
        //递归出口 以及简单校验
        if (index < 0 || treeArray == null || index >= treeArray.length) {
            return;
        }
        //当前节点的左子结点
        int indexLeft = 2 * index + 1;
        //当前节点的右子节点
        int indexRight = 2 * index + 2;
        //假设传入的当前节点（父结点）是最大的
        int maxIndex = index;

        //两次比较都在数组不越界的情况下运行
        //比较左子结点和父结点的值
        if (indexLeft < treeArray.length && treeArray[indexLeft] > treeArray[maxIndex]) {
            //如果左子结点的值比较大，替换最大结点
            maxIndex = indexLeft;
        }
        //比较右子结点和父结点的值
        if (indexRight < treeArray.length && treeArray[indexRight] > treeArray[maxIndex]) {
            //如果右子结点的值比较大，替换最大结点
            maxIndex = indexRight;
        }
        //经过这两次比较后，maxIndex会成为真正的最大
        //交换最大的节点与父结点的位置 如果最大节点依然是初始的index 就不交换
        if (maxIndex!=index){
            swap(treeArray, index, maxIndex);
            //注意这里的递归 注意这里index是maxIndex 因为交换后，maxIndex位置的子结点会发生改变 这会破坏子结点所在子树的堆特性。
            heapify(treeArray, maxIndex);
        }
    }

    /**
     * 堆化 堆化一颗无序树 大顶堆
     * @param treeArray 数组形式的树
     */
    public void buildHeap(int[] treeArray) {
        //拿到最后一个节点的下标
        int lastNodeIndex = treeArray.length - 1;
        //找到最后一个节点的父结点 从此节点开始向上堆化即可
        int lastParentIndex = (lastNodeIndex - 1) / 2;
        //开始堆化 对每个非叶子节点所在的子树进行堆化
        for (int i=lastParentIndex;i>=0;i--){
            //调用堆化子树的方法
            heapify(treeArray,i);
        }
    }

}

//堆化测试
class HeapSortingTest {
    public static void main(String[] args) {
        int[] treeArray = {2, 5, 3, 1, 10, 4};
        HeapSorting heapSorting = new HeapSorting();
        heapSorting.buildHeap(treeArray);
        System.out.println(Arrays.toString(treeArray));
    }
}

排序

在弄明白了堆化之后，堆排序就会变得非常之简单。

堆排序的做法是：

将堆的根节点与最后一个结点交换位置，这样最后一个节点就是堆的最值，随后把最后一个结点剔除堆，然后再对被打乱的堆进行一次堆化，如此循环，依次被剔除堆的结点就会排成一个有序的队列。

如何表示结点被剔除了堆呢？

我们可以每轮循环时移出堆中要被剔除的元素，但有个更好的方法：

使用一个常数n表示堆中结点的总数，而n恰好决定了每轮堆化最后一个非叶子节点，我们只需要每轮让n-1，就能做出剔除最后一个节点的效果，这样做完后，不需要额外的空间，就能完成堆排序。

由于第一次堆化后已经是一个堆了，所以把第一次堆化单独进行，然后循环对每轮的二叉树根结点，调用heapify方法即可，该方法会堆化传入index的结点的子树，并且递归堆化被上一次堆化影响的子树。

堆排序代码实现

注意，增加了参数n来表示节点数量，变动了原来的一些堆化代码

java完整代码

package Sort;

import java.util.Arrays;

public class HeapSorting {


    /**
     * 交换两个结点的位置
     *
     * @param treeArray 一个数组
     * @param index1    数组位置1
     * @param index2    数组位置2
     */
    public void swap(int[] treeArray, int index1, int index2) {
        //临时变量
        int temp = treeArray[index1];
        treeArray[index1] = treeArray[index2];
        treeArray[index2] = temp;
    }


    /**
     * 堆化核心方法 堆化子树 大顶堆 对一个节点做heapify的时候，必须保证它的所有子树都已经是堆。
     *
     * @param treeArray 数组形式的树
     * @param index     从index号位开始堆化
     * @param n         堆中结点数
     */
    public void heapify(int[] treeArray, int index, int n) {
        //递归出口 以及简单校验
        if (index < 0 || treeArray == null || index >= n) {
            return;
        }
        //当前节点的左子结点
        int indexLeft = 2 * index + 1;
        //当前节点的右子节点
        int indexRight = 2 * index + 2;
        //假设传入的当前节点（父结点）是最大的
        int maxIndex = index;
        
        //两次比较都在数组不越界的情况下运行
        //比较左子结点和父结点的值
        if (indexLeft < n && treeArray[indexLeft] > treeArray[maxIndex]) {
            //如果左子结点的值比较大，替换最大结点
            maxIndex = indexLeft;
        }
        //比较右子结点和父结点的值
        if (indexRight < n && treeArray[indexRight] > treeArray[maxIndex]) {
            //如果右子结点的值比较大，替换最大结点
            maxIndex = indexRight;
        }
        //经过这两次比较后，maxIndex会成为真正的最大
        //交换最大的节点与父结点的位置 如果最大节点依然是初始的index 就不交换
        if (maxIndex != index) {
            swap(treeArray, index, maxIndex);
            //注意这里的递归 注意这里index是maxIndex 因为交换后，maxIndex位置的子结点会发生改变 这会破坏子结点所在子树的堆特性。
            heapify(treeArray, maxIndex, n);
        }
    }

    /**
     * 堆化 堆化一颗无序树 大顶堆
     *
     * @param treeArray 数组形式的树
     * @param n         堆中结点数
     */
    public void buildHeap(int[] treeArray, int n) {
        //拿到最后一个节点的下标
        int lastNodeIndex = n - 1;
        //找到最后一个节点的父结点 从此节点开始向上堆化即可
        int lastParentIndex = (lastNodeIndex - 1) / 2;
        //开始堆化 对每个非叶子节点所在的子树进行堆化
        for (int i = lastParentIndex; i >= 0; i--) {
            //调用堆化子树的方法
            heapify(treeArray, i, n);
        }
    }

    /**
     * 堆排序
     *
     * @param treeArray 数组形式的树
     */
    public void HeapSort(int[] treeArray) {
        //n的初始值为堆的节点总数
        int n = treeArray.length;
        //对无序数组堆化
        buildHeap(treeArray, n);
        //堆排序 lastNodeIndex为最后一个节点的下标 递减
        for (int lastNodeIndex = n - 1; lastNodeIndex > 0; lastNodeIndex--) {
            //交换堆中第一个结点和最后一个结点
            swap(treeArray, 0, lastNodeIndex);
            //每轮从根节点进行子树堆化即可 此时每轮模拟的结点数 刚好等于lastNodeIndex
            heapify(treeArray, 0, lastNodeIndex);
        }
    }
}

//堆排序测试
class HeapSortingTest {
    public static void main(String[] args) {
        int[] treeArray = {0, 7, 4, 6, 3, 1, 2, 9, 8, 5};
        HeapSorting heapSorting = new HeapSorting();
        heapSorting.HeapSort(treeArray);
        System.out.println(Arrays.toString(treeArray));
    }
}

输出

D:\java\bin\java.exe "-javaagent:D:\idea\IntelliJ IDEA 
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Process finished with exit code 0

写在最后

堆排序到此便总结完成~！

可喜可贺，断断续续的写了很长时间。虽然现在回过头来看，当时代码写得很不成熟，不过也能看到一些进步，回顾完这些数据结构和常见算法后，便能开始leetCode无尽地域刷题之旅了。到时候也会更新leetCode的内容。

反思

正好在这时，看到一个比较引发思考的文章，这是我在学习Go语言时看到的，原文：https://www.imooc.com/article/19963

二分查找，这是一个看似简单实则很难的问题，因为需要考虑的事情很多，一段二分查找的代码大概率的就会出现层出不穷的bug：

D.Knuth：Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky

即使二分查找的思想相对来说很直接简单，但具体实现起来有特别多的注意点。

比如，据说Java库里面的二分查找，曾经有一个埋藏了10年才被修复的bug：

• 当时java库二分查找的源码

public static int binarySearch(int[] a, int key) {
        int low = 0;
        int high = a.length - 1;
        while (low <= high) {
            int mid = (low + high) / 2;
            int midVal = a[mid];
            if (midVal < key)
                low = mid + 1;
            else if (midVal > key)
                high = mid - 1;
            else
                return mid;// key found
        }
        return -(low + 1);// key not found.
    }

int mid = (low + high) / 2;中，low + high 是会溢出的

修复后的写法：

• int mid = (low + high) >>> 1; 三个>表示无符号位移的意思。

这样或许也可行

• mid = low + (high - low) / 2

写二分算法时，应该多考虑以下几点：

ccmouse：

1. 差1错误。我们的左端点应该是当前可能区间的最小范围，那么右端点是最大范围呢，还是最大范围+1呢。我们取了中间值之后，在缩小区间时，有没有保持左右端点的这个假设的一致性呢？

2. 死循环。我们做的是整数运算，整除2了之后，对于奇数和偶数的行为还不一样，很有可能有些情况下我们并没有减小取值范围，而形成死循环。

3. 退出条件。到底什么时候我们才觉得我们找不到呢？

请让自己的代码出现尽量少的bug吧