数据结构_栈

发表于 | 更新于 | 分类于

数据结构与算法

栈Stack、逆波兰表达式Reverse Polish Notation

1. 栈

栈的示意图：

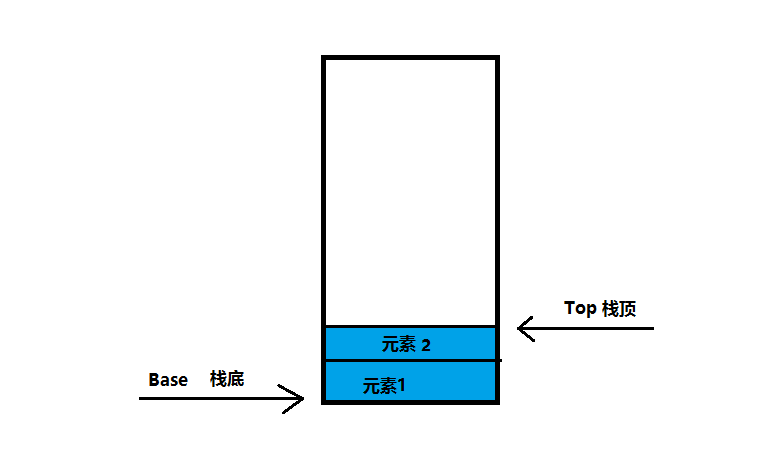
  • 只操作栈顶元素，栈底不变
  • 每次元素进栈，top上移；元素出栈，top下移
  • 所以晚进栈的元素，会先出栈
  • 栈滿的条件
    • top==Maxsize-1（Maxsize是初始化数组的值）
  • 栈空的条件
    • top==-1（即初始状态）

tips：

我们已经分析过了队列，与队列进行比较。

Java实现

可以用数组实现，也可以用链表，类比队列的实现，较为简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
package Stack;

import java.util.Scanner;

/**
 * 栈的数组方式实现
 */
public class ArrayStack {

    int MaxSize = 0;//最大容量
    int top = -1;//栈顶指针
    int base = -1;//栈底
    int[] array;//数组

    public ArrayStack(int maxSize) {//初始化栈
        MaxSize = maxSize;
        array = new int[MaxSize];
    }

    //判断栈滿
    public boolean isFull() {
        return top == MaxSize - 1;
    }

    //判断栈空
    public boolean isEmpty() {
        return top == base;
    }

    //元素入栈
    public void push(int node) {
        if (isFull()) {
            System.out.println("栈滿");
        } else {
            top++;//top上移
            array[top] = node;
        }
    }

    //元素出栈
    public int pop() {
        if (isEmpty()) {
            throw new RuntimeException("栈为空");
        } else {
            int value = array[top];
            top--;
            return value;
        }
    }

    //显示当前的栈顶元素
    public int showTop() {
        if (isEmpty()) {
            throw new RuntimeException("为空");
        } else {
            return array[top];
        }
    }

    //打印栈
    public void show() {
        if (isEmpty()) {
            System.out.println("为空");
        } else {
            for (int i = 0; i <= top; i++) {//从0遍历到top即可
                System.out.println(array[i]);
            }
        }
    }

}

class ArrayStackDemo {
    public static void main(String[] args) {
        ArrayStack stack = new ArrayStack(5);
        boolean loop = true;
        String key = "";
        Scanner scanner = new Scanner(System.in);

        while (loop) {
            System.out.println("show: 表示显示栈");
            System.out.println("exit: 退出程序");
            System.out.println("push: 表示添加数据到栈(入栈)");
            System.out.println("pop: 表示从栈取出数据(出栈)");
            System.out.println("showTop: 表示显示当前栈顶的数据");
            System.out.println("请输入你的选择");
            key = scanner.next();
            switch (key) {
                case "show":
                    stack.show();
                    break;
                case "push":
                    System.out.println("请输入一个数");
                    int value = scanner.nextInt();
                    stack.push(value);
                    break;
                case "pop":
                    try {
                        int res = stack.pop();
                        System.out.printf("出栈的数据是 %d\n", res);
                    } catch (Exception e) {
                        // TODO: handle exception
                        System.out.println(e.getMessage());
                    }
                    break;
                case "showTop":
                    try {
                        int res = stack.showTop();
                        System.out.printf("出栈的数据是 %d\n", res);
                    } catch (Exception e) {
                        // TODO: handle exception
                        System.out.println(e.getMessage());
                    }
                    break;
                case "exit":
                    scanner.close();
                    loop = false;
                    break;
                default:
                    break;
            }
        }
        System.out.println("程序退出~~~");
    }
}

2. 逆波兰表达式

前缀表达式

前缀表达式是一种没有括号的算术表达式，与中缀表达式不同的是，其将运算符写在前面，操作数写在后面，又称波兰表达式，如：

1
- + 1 * + 2 3 4 5

中缀表达式

中缀表达式是我们生活中常见的表达式，如：

1
1+((2+3)*4)-5

后缀表达式

与前缀表达式相反，把运算符写在后面，操作数写在前面，又称逆波兰表达式，后缀表达式更加利于计算机的执行，所以常常把中缀表达式转成后缀表达式来执行。后缀表达式的例子，如：

1
1 2 3+4*+5-

中缀表达式–>后缀表达式的转换

假如给定中缀表达式：

1
1+((2+3)*4)-5

中缀表达式转成后缀表达的算法：

  1. 初始化两个栈：运算符栈s1和储存中间结果的栈s2；
  2. 从左至右扫描中缀表达式；
  3. 遇到操作数时，将其压s2；
  4. 遇到运算符时，比较其与s1栈顶运算符的优先级：
    • 如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
    • 否则，若优先级比栈顶运算符的高，也将运算符压入s1；
    • 否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4-1)与s1中新的栈顶运算符相比较；
  5. 遇到括号时：
    • 如果是左括号“(”，则直接压入s1
    • 如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
  6. 重复步骤2至5，直到表达式的最右边
  7. 将s1中剩余的运算符依次弹出并压入s2
  8. 依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

当然，最后也可以不动s1，把s2中的元素压入s1，然后输出s1即可。

上面是引用的资料，说了这么多，总结就这几句话：

  • 在运算符只有+ - * /时（其他情况暂不考虑）
  • 不是运算符也不是括号，那就是字母或数字，直接扔到集合里（栈或队列也行）
  • 扫描到左括号(，直接入符号栈
  • 扫描到右括号)，不让它push入栈，把符号栈里的元素pop弹出并加入集合，直到pop出一个左括号(为止。注意，左括号(不加入集合
  • 扫描到运算符：
    • 与栈顶top的运算符比较优先级，如果top的优先级比较高，弹出top并加入集合，继续看下一个top，如此循环，当top的元素优先级低时，就入栈。
    • 栈为空时，当然是直接入栈；top是左括号(时，无视它，也直接入栈。

java实现

将以下字符串转换成逆波兰表达式：

    • 1+((2+3)*4)-5
    • 22*(94+6/31-513)+44
    • aa*(s+ad+c)-d
    • 3A*(2b+5a+abc)-3abcd

转换支持字母和数字的组合，运算符只考虑+-*/，数字暂时只考虑正整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
package Stack;

import com.sun.org.apache.xpath.internal.operations.Operation;

import java.util.*;

public class ReversePolishNotationCalculator {//关于逆波兰表达式的计算器


    //运算符栈
    Stack stack = new Stack();
    //输出集合
    List<String> list = new ArrayList<>();

    //自定义运算符优先级
    HashMap<String, Integer> hashMap = new HashMap<String, Integer>() {
        {
            //用map把运算符对应一个int值，模拟优先级
            put("+", 0);
            put("-", 0);
            put("*", 1);
            put("/", 1);
            //战术性把左括号当成优先级最低的运算符
            put("(", -1);

        }
    };

    //获取运算符优先级，（自定义的）
    public int getOperatorPrecedence(String operator) {
        return hashMap.get(operator);
    }

    //匹配字母,判断是否是字母的方法,这样可以转换a*(b+c)-d这样的表达式
    public boolean isABC(String value) {
        return value.matches("[a-zA-Z]+");
    }

    //匹配字母，比较ascii码的方式
    public boolean isABC(int value) {
        return 97 <= value && value <= 122 || 65 <= value && value <= 90;
    }

    //匹配数字,查看value是不是匹配数字
    public boolean isNum(String value) {
        return value.matches("\\d+");
    }

    //匹配数字，比较ascii码的方式
    public boolean isNum(int value) {
        return 48 <= value && value <= 57;
    }

    //确认是不是+-*/这4个运算符
    public boolean isOperator(String value) {
        return "+".equals(value) || "-".equals(value) || "*".equals(value) || "/".equals(value);
    }


    //循环比较当前运算符与栈顶运算符的优先级
    public void loopCompare(String curOper) {
        //拿到当前运算符的优先级数
        int curP = getOperatorPrecedence(curOper);
        int stackP;
        String pop;
        while (true) {
            if (stack.empty()) {
                stack.push(curOper);
                break;
            }
            //获取栈顶元素的优先级数
            stackP = getOperatorPrecedence((String) stack.peek());
            //如果该运算符的优先级高，将该运算符入栈，结束循环
            if (curP > stackP) {
                stack.push(curOper);
                break;
                //若该运算符优先级低
            } else {
                //将栈中的一个元素pop出，然后加入集合
                pop = (String) stack.pop();
                list.add(pop);
            }

        }
    }

    //将字符串每个字符间添加空格，注意有多位数
    public String addBlank(String expression) {
        //先判断字符串是否为空
        if (expression == null || expression.length() == 0) {
            return null;
        }
        //把字符串转成int数组
        int[] array = expression.codePoints().toArray();
        //全局用的字符串构建器
        StringBuilder sb = new StringBuilder();
        //临时用的
        StringBuilder sbNum = null;
        //临时字符串
        String sbNumString = "";
        //从int型的ASCII值转成字符型
        for (int i = 0; i < array.length; i++) {
            //如果当前值是数字或字母
            if (isNum(array[i]) || isABC(array[i])) {
                //新建一个临时数字字符串构建器
                sbNum = new StringBuilder();
                //临时变量
                int j = i;
                //查看下一个是不是也是数字或字母
                while (true) {
                    //已经到数组最大长度时（说明一直到最后都是数字和字母），把最后一个数字\字母拼进来，让i遍历完成
                    if (j == array.length - 1) {
                        sbNum.append((char) array[j]);
                        i = j + 1;
                        break;
                    }
                    //当前值不是数字也不是字母时，把i改为j的值，跳出循环
                    if (!isNum(array[j]) && !isABC(array[j])) {
                        i = j - 1;
                        break;
                    }
                    //临时拼接
                    sbNum.append((char) array[j]);
                    j++;
                }
                //结束循环后，说明一个完整的数字\字母已经拼接完成
                sbNumString = sbNum.toString();
                //拼入全局字符串
                sb.append(sbNumString + " ");
            } else {
                //如果不是数字或字母，直接拼接
                sb.append((char) array[i] + " ");
            }

        }
        return sb.toString();
    }


    //把输入的中缀表达式字符串，转为逆波兰表达式，这是表达式中字符有空格隔开的情况
    public String convertorWithBlank(String expression) {
        //先判断字符串是否为空
        if (expression == null || expression.length() == 0) {
            return null;
        }
        //去除字符串头尾的空格
        String expressionTrim = expression.trim();
        //按空格拆分出一个字符串数组
        String[] strings = expressionTrim.split(" ");

        //不进行运算，不用转int
        for (String value : strings) {

            if (isOperator(value)) {
                //是运算符的话，去循环比较优先级
                loopCompare(value);
                //如果是左括号
            } else if ("(".equals(value)) {
                //压入栈
                stack.push(value);
                //如果是右括号
            } else if (")".equals(value)) {
                while (true) {
                    String pop = (String) stack.pop();
                    //当pop出左括号时结束循环
                    if ("(".equals(pop)) {
                        break;
                    }
                    //把不是(的运算符加入集合
                    list.add(pop);
                }
                //既不是运算符，也不是括号（设表达式中不包括大括号、中括号、以及除了+—*/以外的运算符等）
            } else {
                //是数字或字母或数字+字母，加入集合
                list.add(value);
            }
        }

        //最后，将栈中剩余的元素加入集合
        while (!stack.empty()) {
            list.add((String) stack.pop());
        }
        //结束后，得到一个包含全部字符的list集合
        //使用StringBuilder构建出字符串
        StringBuilder sb = new StringBuilder();
        for (String m : list) {
            sb.append(m + " ");
        }
        //返回一个和字符串构建器内容相同的字符串
        return sb.toString();
    }


    //把输入的中缀表达式字符串，转为逆波兰表达式，这是不带空格的情况
    public String convertor(String expression) {
        //转成有空格的字符串
        String expressionWithBlank = addBlank(expression);
        //转成后缀表达式（逆波兰表达式）
        return convertorWithBlank(expressionWithBlank);
    }

    
	//转换测试
    public static void main(String[] args) {
       ReversePolishNotationCalculator calculator = new ReversePolishNotationCalculator();

        String expression1 = "1+((2+3)*4)-5";
        String expression2 = "22*(94+6/31-513)+44";
        String expression3 = "aa*(s+ad+c)-d";
        String expression4 = "3A*(2b+5a+abc)-3abcd";

        String converteds1 = calculator.convertor(expression1);
        String converteds2 = calculator.convertor(expression2);
        String converteds3 = calculator.convertor(expression3);
        String converteds4 = calculator.convertor(expression4);

        System.out.println(converteds1);
        System.out.println(converteds2);
        System.out.println(converteds3);
        System.out.println(converteds4);

    }
}

输出结果

1
2
3
4
1 2 3 + 4 * + 5 - 
22 94 6 31 / + 513 - * 44 + 
aa s ad + c + * d - 
3A 2b 5a + abc + * 3abcd -

计算逆波兰表达

经过上面的转换，我们得到一个后缀表达式，计算机计算后缀表达式的算法如下：

从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果

比如，逆波兰表达式：

1
3 4 + 5 × 6 -

后缀表达式是没有括号的，所以对计算机来说，简单了许多，把运算符置后，方便栈运算。

直到了这个逻辑，那么代码实现就很简单了：

java实现

利用中缀–>后缀表达式的代码，我们直接计算中缀表达式，即(3+4)×5-6。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//计算一个中缀表达式的结果，只考虑正整数、+-*/、不包含字母，考虑到操作数长度，全程使用long类型计算
   public Long caculate(String expression) {
       //先判断字符串是否为空
       if (expression == null || expression.length() == 0) {
           return null;
       }
       //把输入的中缀表达式转为逆波兰表达式
       String RPNexpression = convertor(expression);
       //计算逆波兰表达式，注意，转换来的表达式是有空格隔开的
       String[] splits = RPNexpression.split(" ");
       //把栈和集合初始化
       stack = new Stack();
       list = new ArrayList<>();
       //两个参与运算的临时变量
       long numTop;
       long numNext;
       //存储value的long值
       long valueLong;
       //遍历数组
       for (String value : splits) {
           //如果是数字
           if (isNum(value)) {
               //转成long类型后直接入栈
               valueLong = Long.parseLong(value);
               stack.push(valueLong);
               //如果是运算符
           } else if (isOperator(value)) {
               numTop = (long) stack.pop();
               numNext = (long) stack.pop();
               //进行运算,然后把运算后的结果入栈
               stack.push(caculateTopAndNext(numTop, numNext, value));
           } else {
               System.out.println("表达式不合法，并且不能包含字母、小数、负数、以及+-*/以外的其他运算符");
               return null;
           }
       }
       //根据栈内是否为空，空的话返回null，不为空返回栈内元素
       return stack.empty() ? null : (long) stack.pop();
   }

   //测试
   public static void main(String[] args) {
       ReversePolishNotationCalculator calculator = new ReversePolishNotationCalculator();
       Long rs = calculator.caculate("(3+4)*5-6");
       System.out.println(rs);
   }

输出结果

1
29

☘(๑•̀ㅂ•́)و✧预告：

Shirtiny：下篇文章是关于递归的，正在写