单链表、双向链表、单向环形链表

数据结构与算法

链表LinkedList

链表是有序列表，但其在内存中并非有序存储，如单链表：

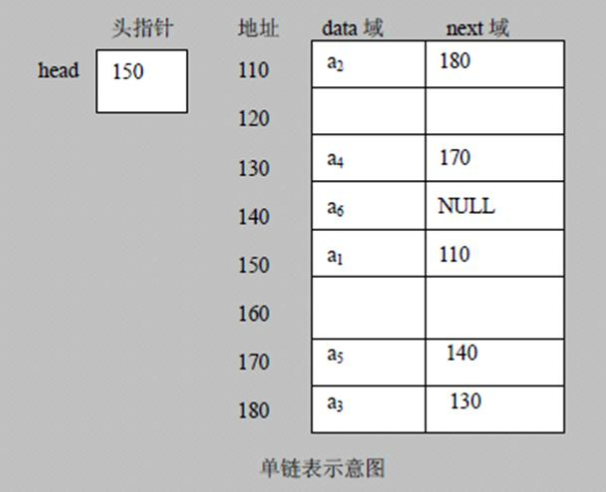
以节点的方式，链式存储。按实际需求，也有无头节点的链表。

1. 单链表SingleLinkedList

单链表逻辑结构：

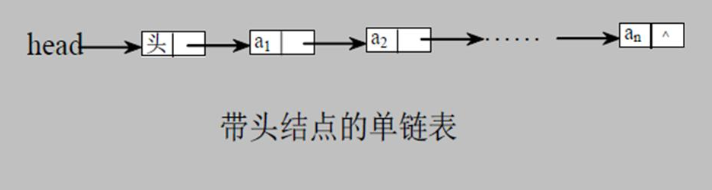
• 每个节点都包含两个域
  • data域，用来存储数据对象
  • next域，指向下一个节点
• head头节点，不存放具体数据，只表示单链表的头，不能移动
• 尾节点，即链表最后的一个节点，next域为null

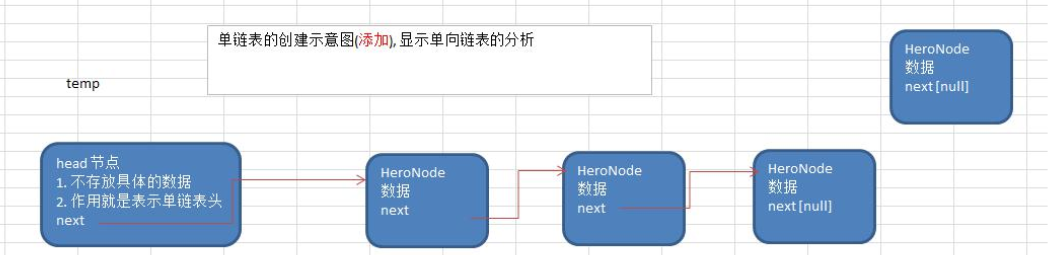
分析

• 首先会创建一个头结点，data域为空，next域为空

• 得出结论，当head头节点的next域为空时，单链表为空

• 向链表中加入一个节点：

  • 找到尾节点
  • 使尾节点的next域指向此节点

• 尾节点的next域始终为空

  • 所以，除了head节点以外，当节点next域为空时，此节点为尾节点

联想

• 考虑节点排序时，向链表加入一个节点：

  • 找到编号大于新加入节点的节点，即满足linkedNode.id>newNode.id的节点

  • 执行插入，将此节点放在新节点的next域，然后把新节点放入上一节点的next域，即

  • newNode.next=linkedNode;
    linkedNode.pre.next=newNode;
    //而实际上linkedNode.pre是不存在的，因为单链表的节点只有next域，不能用当前节点表示上一个节点
    //设linkedNode的上一个节点为preNode==linkedNode.pre
    //则可以把linkedNode表示为pretNode.next，所以上面2个语句为：
    newNode.next=preNode.next;
    preNode.next=newNode;

• 删除一个节点

  • 找到编号等于指定编号的节点，即满足linkedNode.id==deleteId的节点

  • 执行删除，用此节点的后一节点，顶替此节点的位置，即

  • linkedNode.pre.next=linkedNode.next;
    //同理，设linkedNode的上一个节点为preNode==linkedNode.pre，则有：
    preNode.next=preNode.next.next;
    //此时在链表外的linkedNode成了不被引用的对象，会被JVM垃圾回收机制自动回收

• 修改节点信息
  • 根据id找到对应节点，修改data域信息即可。
• 统计单链表内有效节点的个数size
  • 让temp从第一个有效节点head.next开始遍历，计数即可。
• 查找到单链表中倒数第n个节点
  • 需要先获得链表有效节点的个数size
  • 第(size-n+1)个节点，便是倒数第n个节点
• 反转单链表，即：假如有节点为1234的链表，将它反转为4321
  • 创建一个新的头结点newHead，用来作为新链表的头
  • 遍历原链表时，将当前链表的节点放入newHead与newHead后一个节点之间
  • 遍历原链表时，需要保存当前节点的下一个节点，以便返回到原链表
  • 最后遍历完成后，将新节点的第一个有效节点，放入原head节点的next域
• 逆序打印单链表
  • 遍历时，把单链表中节点压入栈中，然后再从栈中取出的节点并打印即可。
• 合并两个有序的单链表，使之仍然有序（示例中为由小到大）
  • 初始化temp1为链表1的第一个有效节点。而temp2为链表2的头结点
  • 将链表1放入链表2中，使temp2不断后移。在找到temp1的插入位置后，temp1才后移。
  • 若直到temp2后移到末尾都没有找到temp1能插入的位置，则把temp1置于temp2末尾，结束循环。
• 取出链表中所有节点的集合
  • 遍历取出，使用List集合
  • 注意，取出时要把每个节点的next域置为空，注意临时保存断掉的链表，以及循环退出条件
• 按顺序批量添加节点
  • foreach遍历上面方法取出的节点集合，然后调用排序添加节点的方法即可。
• 使一个无序链表转换为有序列表（示例中为由小到大）
  • 与上面的方法结合，就可以实现2个无序列表合并到1个有序列表

单链表java实现

Node节点类

package LinkedList;

public class Node {
    //data
    int id;
    String name;
    
    Node next;//next
    Node pre;//pre，单链表不用
    
    //构造器
    public Node() {
    }
    public Node(int id, String name) {
        this.id = id;
        this.name = name;
    }
     public Node(int id, String name, Node next) {
        this.id = id;
        this.name = name;
        this.next = next;
    }
   
    @Override//重写toString方法，注意，无需打印next和pre
    public String toString() {
        return "Node{" +
                "id=" + id +
                ", name='" + name + '\'' +
                '}';
    }
    
     //setter&getter，我在单向链表中直接对属性操作，在双向链表中使用set方法，目的是产生对比，让读者体会方法封装的可读性和便利性。
}

单链表类

package LinkedList;

public class SingleLinkedList {
    private Node headNode=new Node();//头节点
    private Node temp;//设一个过渡节点，初始为头节点


    //获取头节点
    public Node getHeadNode(){
        return this.headNode;
    }

   //判断链表是否为空
    public boolean isNonNode(){
        return headNode.next == null;
    }

    //添加Node(不考虑排序)
    public void addNode(Node node){
        temp=headNode;//初始化temp
        //找到尾节点
        while (true){
            //判断过渡节点的next域是否为空
            if (temp.next==null){
                temp.next=node;
                break;//找到next域为空的节点，便退出循环
            }else {
                //否则temp后移一个节点
                temp=temp.next;
            }
        }

    }
    
    //添加Node，考虑排序
    public void addNodeByOrder(Node node){
        temp=headNode;//初始化temp
        while(true){
            if (temp.next==null){//此时链表为空或已到链表末尾
                //直接添加节点
                temp.next=node;
                break;
            }else if (temp.next.id>node.id){//此时temp与temp.next之间的位置，便是node应该插入的位置
                node.next=temp.next;//将temp.next，变成node的后一个节点
                temp.next=node;//将node，作为temp的后一个节点
                break;
            }else if (temp.next.id==node.id){
                System.out.println("该编号的节点已经存在");
                break;
            }
            temp=temp.next;//以上都不满足，后移temp

        }
        
    //删除节点
    public void deleteNode(int id){
        temp=headNode;//初始化temp
        while (true){
            if (temp.next==null){
                System.out.println("链表中没找到要删除的节点");
                break;
            }else if (temp.next.id==id){
                temp.next=temp.next.next;//用要删除节点的后一个节点，替换要删除的节点
                //不被引用的对象，会被JVM垃圾回收机制自动回收
                System.out.println("删除"+id+"号节点");
                break;
            }
            temp=temp.next;//此次循环未找到符合条件的节点，后移
        }
    }

    //修改节点
    public void updateNode(Node newNode){
        temp=headNode;
        while (true){
            if (temp.next==null){
                System.out.println("链表中没找到要修改的节点");
                break;
            }else if (temp.next.id==newNode.id){
                temp.next.name=newNode.name;
                break;
            }
            temp=temp.next;
        }
    }
        
    //打印链表
    public void show(){
        //当链表为空时，直接提示链表为空
        if (isNonNode()){
            System.out.println("当前单链表为空");
        }else {
            temp=headNode;//初始化temp
            while (true){
                temp=temp.next;//temp后移
                if (temp==null){//到尾节点的next时结束
                    break;
                }
                System.out.println(temp);//输出此时temp的值
            }
        }
    }
        
    //获取链表有效节点个数
    public int getSize(){
        temp=headNode.next;//初始化temp，注意，这次初始temp的值为头节点的下一个节点，即第一个有效节点
        int size=0;
        while (true){
            if (temp==null){
                break;
            }
            size++;
            temp=temp.next;
        }
        return size;
    }

	//查找到倒数第n个节点，方案①
    public Node getLastIndexOf(int n){
        int size=getSize();
        if (isNonNode()||n<=0||n>size){
            System.out.println("没有找到该编号的节点");
            return null;
        }
        temp=headNode;
        int i=0;
        while (true){
            i++;
            temp=temp.next;
           if (i==(size-n+1)){//第一次循环时，i与temp为0和head，第二次时i与temp为1和第一个有效节点，所以i可以作为有效节点的坐标
               return temp;
           }
        }
    }
   	//或使用for循环
    /*
    temp=headNode.next;//这里把temp设为了第一个有效节点，i= size - index时结束循环。当然，也可以同上面while一样设为head，i= size - index+1时结束循环。
		for(int i =0; i< size - index; i++) {
        cur = cur.next;
    }
		return cur;
    */       
        
               
    //反转单向链表
    public void  reverseLinkedList(){
        if (headNode.next==null||headNode.next.next==null){
            System.out.println("当前链表为空，或只有一个节点，不需要反转");
            return;
        }

        temp=headNode.next;//初始化temp为第一个有效节点
        Node nextNode;//存储当前节点的下一个节点
        Node newHead =new Node();//新的头结点
        while (true){
            if (temp==null){//循环到temp为空
                break;
            }
            nextNode=temp.next;//把当前节点的下一个节点存起来
            temp.next=newHead.next;//把新head的后一位节点，交给当前节点的next域
            newHead.next=temp;//把当前节点，交给新head的next域
            temp=nextNode;//让temp回到原链表上，后移一位
        }
        headNode.next=newHead.next;//把新合成的链表的第一个有效节点，交给原来的head的next域
        
    }
        
    //逆序打印单向链表
    public void reversePrintList(){
        temp=headNode.next;
        if (isNonNode()){
            System.out.println("链表为空");
        }else {
            Stack<Node> nodeStack=new Stack<>();//创建栈对象
            while (true){
                if (temp==null){
                    break;
                }
                nodeStack.push(temp);//把节点压入栈
                temp=temp.next;//节点后移
            }
            while (nodeStack.size()>0){
                System.out.println(nodeStack.pop());//从栈中取出节点并打印
            }

        }
    }

        
    //合并两个有序的单链表，使之仍然有序
    public SingleLinkedList compound2LinkedList(SingleLinkedList list1,SingleLinkedList list2){
        Node temp1= list1.temp=list1.headNode.next;//第一个有效节点
        Node temp2 =list2.temp=list2.headNode;//头结点
        //把链1放入链2中
        Node head2= list2.headNode;//2链的head，没用到
        Node next1;//1链的临时存储节点
        while (true){
            if (temp1==null&&temp2.next==null){
                break;
            }
            if (temp1!=null){
                next1=temp1.next;//临时保存1链当前节点的下一个节点
                if (temp2.next==null){//temp2.next走到头，也没发现大于temp1的数
                    System.out.println("此后的链2一直小于链1的某个数，由于是有序列表，所以此后链2一直小于链1，直接将把链1放在链2的后面即可");
                    temp2.next=temp1;//把当前temp1的值，挂在temp2的尾部
                    break;
                }
                if (temp2.next.id>=temp1.id){
                    temp1.next=temp2.next;
                    temp2.next=temp1;
                    temp1=next1;//直到temp2符合条件，temp1才后移
                }
            }
            temp2=temp2.next;//temp2始终后移，注意，此时的temp2这条链应该为部分list1与全部list2的混合

        }

        return list2;
    }


    //取节点集合
    public List<Node> getNodes(SingleLinkedList list){
        Node temp=list.temp=list.headNode.next;//初始化temp为该链表的第一个有效节点
        List<Node> nodeList=new ArrayList<>();//新建一个node集合
        Node next=new Node();//初始一个next对象用于存储temp.next
        while (true){
            if (next==null){//当next为空时，退出循环
                break;
            }
            next=temp.next;//将temp的下一个节点临时保存，即保存temp节点以后的链表
            temp.next=null;//将temp的next域设为null
            nodeList.add(temp);//将temp加入节点集合
            temp=next;//将temp重新回到链表上
        }
        return nodeList;
    }
        
        
    //按顺序批量添加节点
    public  void addNodesByOrder(List<Node> nodes){
        temp=headNode;//初始化temp
        for (Node node :nodes) {
            addNodeByOrder(node);//调用排序添加单个node的方法
        }

    }
        
        
     //将一个无序链表转为有序链表
    public SingleLinkedList formatLinkedList(SingleLinkedList list1){
        List<Node> nodes = getNodes(list1);
        SingleLinkedList list2=new SingleLinkedList();
        list2.addNodesByOrder(nodes);
        return list2;
    } 
        
        
        
    //测试
    public static void main(String[] args) {
        //生成无序列表1
        SingleLinkedList singleLinkedList1=new SingleLinkedList();
        singleLinkedList1.addNode(new  Node(1,"1号节点"));
        singleLinkedList1.addNode(new  Node(9,"9号节点"));
        singleLinkedList1.addNode(new  Node(2,"2号节点"));
        singleLinkedList1.addNode(new  Node(4,"4号节点"));
        System.out.println("**********无序链表1");
        singleLinkedList1.show();

        //序列化无序链表1
        SingleLinkedList linkedList1 = singleLinkedList1.formatLinkedList(singleLinkedList1);
        System.out.println("**********转换成有序链表1");
        linkedList1.show();

        //生成无序列表2
        SingleLinkedList singleLinkedList2=new SingleLinkedList();
        singleLinkedList2.addNode(new  Node(2,"2号节点"));
        singleLinkedList2.addNode(new  Node(9,"9号节点"));
        singleLinkedList2.addNode(new  Node(6,"6号节点"));
        singleLinkedList2.addNode(new  Node(1,"1号节点"));
        System.out.println("**********无序链表2");
        singleLinkedList2.show();

        //序列化无序链表2
        SingleLinkedList linkedList2 = singleLinkedList2.formatLinkedList(singleLinkedList2);
        System.out.println("**********转换成有序链表2");
        linkedList2.show();

        //合并两个有序列表，用哪个对象都行
        SingleLinkedList list = linkedList1.compound2LinkedList(linkedList1, linkedList2);
        System.out.println("**************两个有序列表合并后的链表");
        list.show();

    }
}

输出结果：

**********无序链表1
Node{id=1, name='1号节点'}
Node{id=9, name='9号节点'}
Node{id=2, name='2号节点'}
Node{id=4, name='4号节点'}
**********转换成有序链表1
Node{id=1, name='1号节点'}
Node{id=2, name='2号节点'}
Node{id=4, name='4号节点'}
Node{id=9, name='9号节点'}
**********无序链表2
Node{id=2, name='2号节点'}
Node{id=9, name='9号节点'}
Node{id=6, name='6号节点'}
Node{id=1, name='1号节点'}
**********转换成有序链表2
Node{id=1, name='1号节点'}
Node{id=2, name='2号节点'}
Node{id=6, name='6号节点'}
Node{id=9, name='9号节点'}
**************两个有序列表合并后的链表
Node{id=1, name='1号节点'}
Node{id=1, name='1号节点'}
Node{id=2, name='2号节点'}
Node{id=2, name='2号节点'}
Node{id=4, name='4号节点'}
Node{id=6, name='6号节点'}
Node{id=9, name='9号节点'}
Node{id=9, name='9号节点'}

Process finished with exit code 0

2. 双向链表DoublyLinkedList

双向链表逻辑结构：

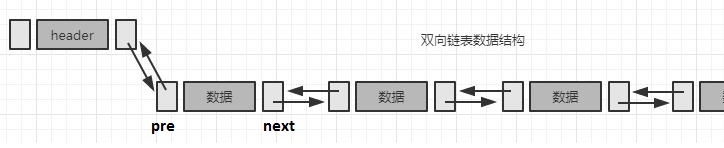
参照单向链表，双向链表在单向链表的基础上，在每个节点多了一个pre域，指向上一个节点。

• 双向链表中的节点可以获取父节点
• 增删时需要把next域和pre域都修改
• 按顺序增加时，即插入操作：
  • 修改pre和next时，注意执行顺序
  • 先让node的pre和next分别连到temp和temp.next
  • 然后将temp.next的pre连到node
  • 最后才将temp的next连到node，否则会找不到原先的temp.next
• 由于过渡节点temp可以指向上一个节点，方便了操作，所以删除时temp可以初始为第一个有效节点：
  • 此时temp为要删除的节点，temp.pre和temp.next的中间是temp。
  • 将temp.next的pre连到temp.pre，把temp.pre的next连到temp.next。
  • 还要注意，当要删除的节点为尾节点时，temp.next.set()会造成空指针异常

我们之前已经详细的分析了单向链表，其余请对照单向链表思考，修改代码。

双向链表java实现

package LinkedList;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class DoublyLinkedListTest {//双向链表的测试类

    public static void main(String[] args) {
        DoublyLinkedList linkedList=new DoublyLinkedList();
        linkedList.addNodeByOrder(new Node(1,"1hao"));
        linkedList.addNodeByOrder(new Node(3,"3hao"));
        linkedList.addNodeByOrder(new Node(2,"2hao"));
        linkedList.addNodeByOrder(new Node(4,"4hao"));
//        linkedList.show();
        List<Node> nodes = getNodes(linkedList);
        DoublyLinkedList list=new DoublyLinkedList();
        list.addNodesByOrder(nodes);
        list.show();


    }



    //反转单向链表
    public static void  reverseLinkedList(DoublyLinkedList list){
        Node headNode = list.getHeadNode();
        Node temp;
        if (headNode.next==null||headNode.next.next==null){
            System.out.println("当前链表为空，或只有一个节点，不需要反转");
            return;
        }

        temp=headNode.next;//初始化temp为第一个有效节点
        Node nextNode;//存储当前节点的下一个节点
        Node newHead =new Node();//新的头结点
        while (true){
            if (temp==null){//循环到temp为空
                break;
            }
            nextNode=temp.next;//把当前节点的下一个节点存起来
            temp.next=newHead.next;//把新head的后一位节点，交给当前节点的next域
            newHead.next=temp;//把当前节点，交给新head的next域
            temp=nextNode;//让temp回到原链表上，后移一位
        }
        headNode.next=newHead.next;//把新合成的链表的第一个有效节点，交给原来的head的next域

    }

    //逆序打印单向链表
    public static void reversePrintList(DoublyLinkedList list){
        Node headNode = list.getHeadNode();
        Node temp=headNode.next;
        if (list.isNonNode()){
            System.out.println("链表为空");
        }else {
            Stack<Node> nodeStack=new Stack<>();//创建栈对象
            while (true){
                if (temp==null){
                    break;
                }
                nodeStack.push(temp);//把节点压入栈
                temp=temp.next;//节点后移
            }
            while (nodeStack.size()>0){
                System.out.println(nodeStack.pop());//从栈中取出节点并打印
            }

        }
    }

    //合并两个有序的单链表，使之仍然有序
    public static DoublyLinkedList compound2LinkedList(DoublyLinkedList list1,DoublyLinkedList list2){
        Node temp1= list1.temp=list1.headNode.next;//第一个有效节点
        Node temp2 =list2.temp=list2.headNode;//头结点
        //把链1放入链2中
        Node head2= list2.headNode;//2链的head，没用到
        Node next1;//1链的临时存储节点
        while (true){
            if (temp1==null&&temp2.next==null){
                break;
            }
            if (temp1!=null){
                next1=temp1.next;//临时保存1链当前节点的下一个节点
                if (temp2.next==null){//temp2.next走到头，也没发现大于temp1的数
                    System.out.println("此后的链2一直小于链1的某个数，由于是有序列表，所以此后链2一直小于链1，直接将把链1放在链2的后面即可");
                    temp2.next=temp1;//把当前temp1的值，挂在temp2的尾部
                    break;
                }
                if (temp2.next.id>=temp1.id){
                    temp1.next=temp2.next;
                    temp2.next=temp1;
                    temp1=next1;//直到temp2符合条件，temp1才后移
                }
            }
            temp2=temp2.next;//temp2始终后移，注意，此时的temp2这条链应该为部分list1与全部list2的混合

        }

        return list2;
    }



    //取节点集合
    public static List<Node> getNodes(DoublyLinkedList list){
        Node temp=list.temp=list.headNode.next;//初始化temp为该链表的第一个有效节点
        List<Node> nodeList=new ArrayList<>();//新建一个node集合
        Node next=new Node();//初始一个next对象用于存储temp.next
        while (true){
            if (next==null){//当next为空时，退出循环
                break;
            }
            next=temp.next;//将temp的下一个节点临时保存，即保存temp节点以后的链表
            temp.next=null;//将temp的next域设为null
            temp.pre=null;
            nodeList.add(temp);//将temp加入节点集合
            temp=next;//将temp重新回到链表上
        }
        return nodeList;
    }



    //将一个无序链表转为有序链表
    public static DoublyLinkedList formatLinkedList(DoublyLinkedList list1){
        List<Node> nodes = getNodes(list1);
        DoublyLinkedList list2=new DoublyLinkedList();
        list2.addNodesByOrder(nodes);
        return list2;
    }


}
//********************************************

    //双向链表类
 class DoublyLinkedList {

        Node headNode=new Node();//头节点
        Node temp;//设一个过渡节点，初始为第一个有效节点



        //获取头节点
        public Node getHeadNode(){
            return headNode;
        }

        public boolean isNonNode(){
            return headNode.next == null;
        }

        //添加Node(不考虑排序)
        public void addNode(Node node){

            temp=headNode;//初始化temp
            //找到尾节点
            while (true){
                //判断过渡节点的next域是否为空
                if (temp.next==null){
                    //将node加入链表
                    temp.setNext(node);
                    node.setPre(temp);

                    break;//找到next域为空的节点，便退出循环
                }else {
                    //否则temp后移一个节点
                    temp=temp.getNext();
                }
            }

        }

        //添加Node，考虑排序
        public void addNodeByOrder(Node node){
            temp=headNode;//初始化temp
            while(true){
                if (temp.next==null){//此时链表为空或已到链表末尾
                    //直接添加节点
                    temp.setNext(node);
                    node.setPre(temp);
                    break;
                }else if (temp.next.id>node.id) {//此时temp与temp.next之间的位置，便是node应该插入的位置
                    node.setPre(temp);//先让node的pre连到temp
                    node.setNext(temp.next);//node的next连到temp.next
                    temp.next.setPre(node);//然后先把temp.next的pre连到node
                    temp.setNext(node);//最后把temp的next连到node

                    break;
                }
                temp=temp.next;//以上都不满足，后移temp

            }



        }

        //按顺序批量添加节点
        public  void addNodesByOrder(List<Node> nodes){
            temp=headNode;//初始化temp
            for (Node node :nodes) {
                addNodeByOrder(node);//调用排序添加单个node的方法
            }

        }


        //删除节点
        public void deleteNode(int id){
            temp=headNode.getNext();//初始化temp为第一个有效节点
            while (true){
                if (temp==null){
                    System.out.println("链表中没找到要删除的节点");
                    break;
                }else if (temp.id==id){
                    if (temp.next==null){
                        temp.pre.setNext(null);//如果节点在最尾部
                        System.out.println("删除"+temp.id+"号节点，该节点是尾节点");
                        break;
                    }
                    temp.next.setPre(temp.pre);//把temp.next的pre连到temp.pre，中间是temp
                    temp.pre.setNext(temp.next);//把temp.pre的next连到temp.next，中间是temp
                    //此时，没有任何节点的next或pre指向temp，不被引用的对象，会被JVM垃圾回收机制自动回收
                    System.out.println("删除"+temp.id+"号节点");
                    break;
                }
                temp=temp.next;//此次循环未找到符合条件的节点，后移
            }
        }

        //修改节点
        public void updateNode(Node newNode){
            temp=headNode;
            while (true){
                if (temp.next==null){
                    System.out.println("链表中没找到要修改的节点");
                    break;
                }else if (temp.next.id==newNode.id){
                    temp.next.name=newNode.name;
                    break;
                }
                temp=temp.next;
            }
        }


        //打印链表
        public void show(){
            //当链表为空时，直接提示链表为空
            if (isNonNode()){
                System.out.println("当前单链表为空");
            }else {
                temp=headNode;//初始化temp
                while (true){
                    temp=temp.next;//temp后移
                    if (temp==null){//到尾节点的next时结束
                        break;
                    }
                    System.out.println(temp);//输出此时temp的值
                }
            }


        }

        //获取链表有效节点个数
        public int getSize(){
            temp=headNode.next;//初始化temp，注意，这次初始temp的值为头节点的下一个节点，即第一个有效节点
            int size=0;
            while (true){
                if (temp==null){
                    break;
                }
                size++;
                temp=temp.next;

            }
            return size;
        }

        //查找到倒数第n个节点
        public Node getLastIndexOf(int n){
            int size=getSize();
            if (isNonNode()||n<=0||n>size){
                System.out.println("没有找到该编号的节点");
                return null;
            }
            temp=headNode;
            int i=0;
            while (true){
                i++;
                temp=temp.next;
                if (i==(size-n+1)){//第一次循环时，i与temp为0和head，第二次时i与temp为1和第一个有效节点，所以i可以作为有效节点的坐标
                    return temp;
                }
            }
        }
        //或使用for循环
    /*
    temp=headNode.next;//这里把temp设为了第一个有效节点，i= size - index时结束循环。当然，也可以同上面while一样设为head，i= size - index+1时结束循环。
		for(int i =0; i< size - index; i++) {
        cur = cur.next;
    }
		return cur;
    */

    }

3. 环形链表

单向环形链表

图示：

这是最简单的形式，除了没有头结点和尾节点外，也没有其他环形结构

• 单个节点的next指向自己，也可以成为环形
• 遍历方法：
  • 设一个指针指向第一个节点，命名为first，该指针位置不变。
  • 设一个移动的指针，初始为first，命名为temp，显然，当temp.next==first时，遍历结束，此时temp表示链表尾部（逻辑上）
  • 遍历前，应当确保temp==first，才能从头遍历
  • 加入新节点时，将链表遍历到尾节点，然后将尾节点的next指向新节点，再把新节点的next指向first。

java实现

package LinkedList;

public class SingleCircleLinkedList {
    private Node first=null;//指向第一个节点
    private Node temp=first;//遍历用的节点，初始为第一个节点

    public void addNode(Node node){
        temp=first;
        while (true){
        if (first==null) {//第一个节点为空，说明链表中没有节点
            node.setNext(node);//单节点环形
            this.first = node;
            this.temp = first;//初始化first和temp
            }else{
            temp=temp.next;//temp后移
            }
            if (temp.next==first){//temp移动后，如果temp.next为first，则说明链表已经遍历到尾部
                temp.setNext(node);
                node.setNext(first);//构造环形
                break;
            }
        }
    }
    
    //根据指定的id 删除该节点
        public void deleteNode(int id) {
        if (isNon()) {
            System.out.println("链表为空");
        } else {
            temp = first;//初始化
            while (true) {
                if (temp.next.id == id) {
                    if (temp.next == first) {//删除的节点为第一个节点
                        //更新first
                        first = temp.next.next;
                    }
                    temp.setNext(temp.next.next);
                    System.out.println("删除节点:" + id);
                    break;
                }
                temp = temp.next;//temp后移
                if (temp == first) {
                    System.out.println("没找到要删除的节点");
                    break;
                }

            }
        }

    }
    
	//打印链表
    public void show(){
        if (first==null){
            System.out.println("链表为空");
        }else {
            temp=first;//初始化temp
            while (true){
                System.out.println(temp);
                if (temp.next==first){
                    break;
                }
                temp=temp.next;//temp后移
            }
        }
    }
}

//测试
class SingleCircleLinkedListTest{
    public static void main(String[] args) {
        SingleCircleLinkedList singleCircleLinkedList=new SingleCircleLinkedList();
        singleCircleLinkedList.addNode(new Node(1,"1hao"));
        singleCircleLinkedList.addNode(new Node(3,"3hao"));
        singleCircleLinkedList.addNode(new Node(4,"4hao"));
        singleCircleLinkedList.addNode(new Node(6,"6hao"));

        singleCircleLinkedList.show();
    }
}

约瑟夫置换

单向链表的实际应用中，约瑟夫问题是非常经典的。下面使用单向环形链表易懂的解决约瑟夫问题，及其变体。

百度百科——约瑟夫问题

分析

• 这里我们依然使用Node节点类，不再新建。
• 需要把N个节点加入链表，并且自动编号
• 从1位置开始计数，temp每后移1次，计数变量i的值就+1
• 删除条件：当计数变量i==m时，删除当前temp指向的节点
  • 要注意，要想删除temp，就需要找到temp.pre，但是单向链表的节点只有next
  • 在i==m-1时，temp.next就是i==m时的要删除的temp。所以只需要在i==m-1时把temp.next删除即可
• 遍历结束条件：链表中只剩一个节点时，即temp.next==tem

java实现

//根据约瑟夫问题删除节点
    public void deleteByJ(int m) {//每次循环中，第m个节点被删除
        if (isNon()) {
            System.out.println("链表为空");
        } else {
            temp = first;//初始为第一个节点
            int i = 1;//计数变量
            while (true) {
                if (temp.next == temp) {//链表中只有一个节点
                    System.out.println("最后一个节点为：" + temp);
                    break;
                }
                if (i == m - 1) {//当数到m号节点的前一个时，删除m节点
                    System.out.println(temp.next.id + "号节点出列");
                    temp.setNext(temp.next.next);//删除节点
                    first = temp.next;//把被删除节点的后一个节点作为第一个节点
                    i = 1;//重置i
                    temp = first;//重置temp为新的first
                } else {
                    temp = temp.next;//temp后移
                    i++;//计数+1
                }
            }
        }
    }

//给定节点总数n，自动编号，组成一个环形
    public void autoAdd(int n) {
        N = n;
        //生成
        for (int i = 1; i <= n; i++) {
            Node node = new Node();
            node.setId(i);
            JosephusList.addNode(node);
        }
    }

//约瑟夫环
class Josephus {
    private SingleCircleLinkedList JosephusList = new SingleCircleLinkedList();//初始队列
    private int N;//总人数
    private int M;//数到M的人出列
    ...
    
//给定数字m，从1号开始数，每次循环数到m的节点出列（删除），直到剩最后一个
    public void run(int m) {
        M = m;
        JosephusList.deleteByJ(m);
    }
}

//测试
class SingleCircleLinkedListTest {
    public static void main(String[] args) {
        Josephus josephus = new Josephus();
        josephus.autoAdd(41);//建立一个总数41的环形链表
        josephus.run(3);//默认从1开始数，数到3的节点出列    
    }
}

运行结果

3号节点出列
6号节点出列
9号节点出列
...
35号节点出列
16号节点出列
最后一个节点为：Node{id=31, name='null'}

约瑟夫问题变体

约瑟夫问题变体很多，解决方式更是多种多样。都在约瑟夫问题的基础上变动，如：

设编号为1,2，··· n的n个人围坐一圈，设编号为k的人从1开始报数，数到m的那个人出列，然后从出列的下一位开始重新从1报数，如此循环，直到只有最后一个人为止，求出队的人的编号序列

相对于原生的约瑟夫问题，这里不在是从1号位置开始报数，而是改成了从k号位置报数，k成了 一个第三方指定的变量。

思路

由于与上个问题区别不大，我们这次换一种不同的思路来解决。

• 注意判断k是否在符合规则的范围内
• 报数前，将first指向k号节点，将temp指向此时first的前一个节点
• 报数时，将first和temp同时移动m-1次，每次移动1位。完成后，此时first就指向需要删除的节点m，temp指向first指向节点的前一个节点
• 把first.next设为新的first节点，然后把first指向temp.next，如此循环即可